Implementation of Eigen faces from Captured images....

The various steps to calculate Eigen faces are


i) Prepare the data:
A 2-D facial image can be represented as 1-D vector by concatenating each row (or column) into a long thin vector.
Let’s suppose we have M vectors of size N (= rows x columns of image) representing a set of sampled images .Then the training set becomes:


ii) Subtract the mean:
The average matrix  has to be calculated, then subtracted from the original faces (i ) and the result stored in the variable

Ψ=1/M∑Mn=1Ѓn [Φ]Xi=fi

iii) Calculate the co-variance matrix

In the next step the covariance matrix A is calculated according to:
A=ΦTΦ



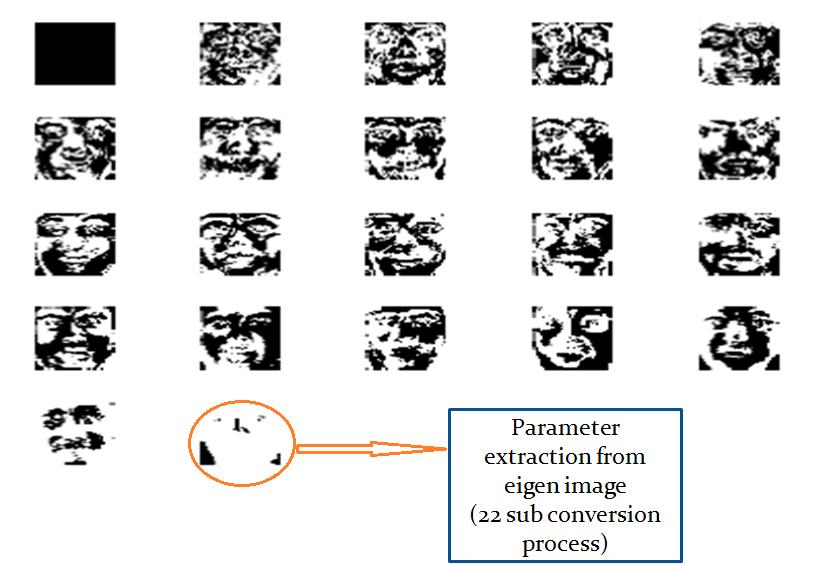
iv) Calculate the Eigenvectors and Eigen values of the covariance matrix. In this step, the Eigen vectors (Eigen vectors) Xi. Calculate Eigen faces
[Φ]Xi=fi

Where, Xi are eigenvectors and fi are Eigen faces.

v) Classifying the faces:
The new image is transformed into its Eigen face components. The resulting weights form the weight vector T : k
Ωk= ΩkT(Гk-ψ)
Where,
k = 1,2,3,4

Tagged in:

• image processing
• biometric
• Advanced Techniques
• future technology