Addition of Consecutive Odd numbers is equal to Square Numbers

Addition of Consecutive Odd numbers is equal to Square Numbers


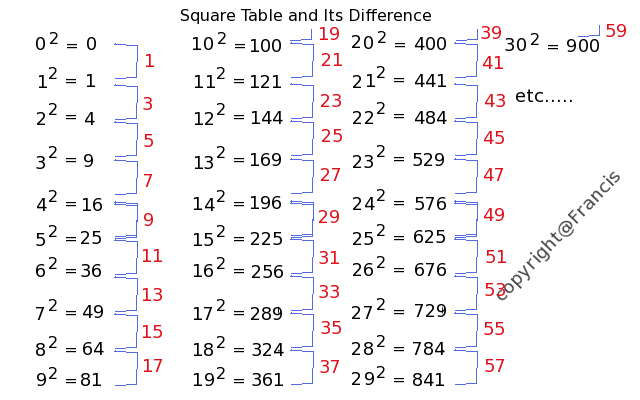In this Square Table To Explain following Properties,
1. Consecutive Odd number Addition is equal to consecutive square value.
2. A square number previous odd number is to multiply that number by 2 and separate by 1
3. A square number next odd number is to multiply that number by 2 and add by 1

Example
If you find 8²,
Previous Odd Number is, 2*8 - 1 = 15
So that, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64

Square Formula:

Proof:
L.H.S = [((a² + b² + 2ab) + (a² + b² - 2ab) ) / 2] - b²
= [(2a² + 2b²) / 2] - b²
= [2(a²+b²) / 2] - b²
= (a²+b²) - b²
= a²
= R.H.S